NINON LIZÉ MASCLEF
Media Artist & Research Scientist
Bloch sphere : Simulation of one qubit
2019-2020
A multi-agent simulation platform for quantum computing.
role
Development, quantum algorithms (Deutsch and Grover) popularization
authors
Franck Assedou, Valérian Coulon, Ninon Lizé Masclef, Yi You
keywords
quantum computing, software, popularization
At the University of Technology of Compiègne, I designed and developed in 2019 an AI distributed simulation platform for quantum computing for popularization purposes. It consisted of a parallelized representation of the quantum circuit of Deutsch-Jozsa algorithm aimed to be distributed on several computers. It was implemented in Java using the multi-agent framework Jade. This is a joint work done with Franck Assedou, Valérian Coulon and Yi You during the course "Multi-agent programming". Check our public repo on GitLab.
Afterwards, I wrote with Franck Assedou a dissertation on quantum computing. The idea was to introduce basic quantum algorithms (Deutsch–Jozsa and Grover) with metaphors, to endow people with some insights about quantum computing with very few mathematical formula. To make quantum computating as accessible as possible, the dissertation is self-contained, which means that all the mathematical concepts mandatory to understand its content, such as complex numbers, are explained in the dissertation. Anyone can read it without any prerequisite. Below is a extract explaining the principle of quantum search achieved through Grover algorithm.
Afterwards, I wrote with Franck Assedou a dissertation on quantum computing. The idea was to introduce basic quantum algorithms (Deutsch–Jozsa and Grover) with metaphors, to endow people with some insights about quantum computing with very few mathematical formula. To make quantum computating as accessible as possible, the dissertation is self-contained, which means that all the mathematical concepts mandatory to understand its content, such as complex numbers, are explained in the dissertation. Anyone can read it without any prerequisite. Below is a extract explaining the principle of quantum search achieved through Grover algorithm.
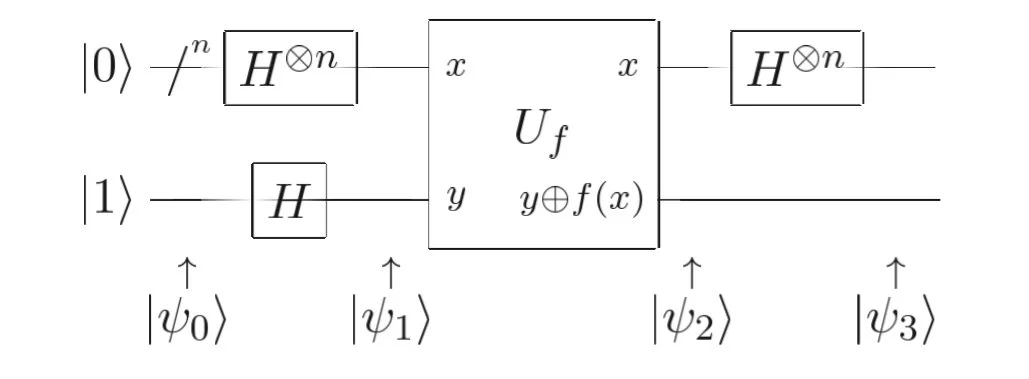
Circuit of Grover algorithm
Quantum Search : Grover algorithm
"Imagine a dictionary of the French language that would be a bit special. Indeed, the words would not be sorted in alphabetical order but they would be put in a totally random order. If we want to know the definition of a word, it might be complicated. If we are extremely lucky, the word we are looking for will be the very first in the dictionary. Conversely, if we are really unlucky, it will be the very last, and in this case, you will have to read all the words in the dictionary before finding the right one.
Finding the right item in a large list of unsorted items - in this case finding the right word among a list of words in a dictionary where words would be placed randomly - is a major search problem. In the classic case, there is not a magic solution, you have to read all the elements one by one until you find the right one. If we imagine that there are n elements in this list, then in the worst case, i.e. when the element we are looking for is the very last, we will have to perform n operations, an operation here being the reading of an item. In theoretical computer science, we say that such a search has a complexity of O(n). Thanks to the parallelism provided by quantum computing, it is possible to perform this search with a complexity of O(√n), namely in about √n operations. To do so, we use Grover's algorithm. Let us imagine that each element of the list has an index, a unique identifier allowing it to be located and which, unlike the elements themselves, would be sorted. For example, imagine that in the dictionary, all the words are unordered but each word has a unique number: the first word in the dictionary is marked by the number 0, the second is marked by the number 1, the third by the number 2 and so on. If we know the index of the word we are looking for, finding it in the dictionary immediately becomes very simple, it is like opening a book on the right page when we know that page. The purpose of Grover's algorithm is to give us this index."
translated from Ninon Lizé Masclef, Franck Assedou (2020). Informatique théorique : de nouvelles méthodes de résolution de problèmes apportées par la mécanique quantique.
Finding the right item in a large list of unsorted items - in this case finding the right word among a list of words in a dictionary where words would be placed randomly - is a major search problem. In the classic case, there is not a magic solution, you have to read all the elements one by one until you find the right one. If we imagine that there are n elements in this list, then in the worst case, i.e. when the element we are looking for is the very last, we will have to perform n operations, an operation here being the reading of an item. In theoretical computer science, we say that such a search has a complexity of O(n). Thanks to the parallelism provided by quantum computing, it is possible to perform this search with a complexity of O(√n), namely in about √n operations. To do so, we use Grover's algorithm. Let us imagine that each element of the list has an index, a unique identifier allowing it to be located and which, unlike the elements themselves, would be sorted. For example, imagine that in the dictionary, all the words are unordered but each word has a unique number: the first word in the dictionary is marked by the number 0, the second is marked by the number 1, the third by the number 2 and so on. If we know the index of the word we are looking for, finding it in the dictionary immediately becomes very simple, it is like opening a book on the right page when we know that page. The purpose of Grover's algorithm is to give us this index."
translated from Ninon Lizé Masclef, Franck Assedou (2020). Informatique théorique : de nouvelles méthodes de résolution de problèmes apportées par la mécanique quantique.